麻雀のデータを統計的に分析してみた話
こんにちは。突然ですが、みなさんは「Mリーグ」をご存じでしょうか。Mリーグは、簡単に言えばAbemaTVで放映されている、4人×8チーム(2021-2022シーズン当時)での団体戦による麻雀のプロリーグです。本記事は、そのMリーグの試合データ・選手データを題材として、麻雀のデータを回帰分析と主成分分析を用いて統計的に分析した結果となります。
1. 扱うデータについて
分析対象のデータとしては、「Mリーグ 2021-2022」のレギュラーシーズン全180試合の試合結果、および同シーズンの選手全32人の成績を選定しました。ここでは、前者の試合データを“df_game”、後者の選手データを“df_player”というデータフレームとして扱い、データフレームの属性(列)は以下に記述した通りです。
☆試合データ“df_game”
- game:試合の通し番号(1~180)
- order:順位(1位~4位)
- team:所属チーム
- player:選手名
- point:得点
- reach:リーチ数
- win:和了数
- deal-in:放銃数
- team-point:試合前のチームの持ち点
- team-order:試合前のチーム順位(1~8)
- team-game:チームでの試合通し番号(1~90)
- prev_point:そのチームの前の得点
☆選手データ“df_player”
- player:選手名
- team:チーム名
- total-match:選手の出場した試合数
- total-game:選手が打った総局数
- point:選手の総獲得ポイント(1000点=1ptで、初めの点からの差分がポイントとなる)
- avg-ranking:平均順位
- first:1位を取った回数
- second:2位を取った回数
- third:3位を取った回数
- forth:4位を取った回数
- top-rate:1位の確率
- top-second-rate:2位以上の確率
- not-last-rate:3位以上の確率
- best-score:シーズンで最も高かった得点
- avg-hit:平均の和了点数
- pon:鳴き率(ポンやチーをした対局の割合)
- reach:リーチした対局の割合
- win:和了した対局の割合
- deal-in:放銃した対局の割合
- avg-deal-in:放銃した点数の平均
2. 試合データの重回帰分析
さて、いよいよ実際の統計データ分析に移ります。試合データを分析するにあたって、「麻雀界の通説を仮説検定する」という目的を設定しました。麻雀に関して、しばしば「流れ」や「ツキ」といったオカルトチックな言説を耳にするため、実際にそういった言説が妥当であるのかを、3つの言説に焦点を当てて、統計的に検証しました。その結果は以下の通りです。
言説1:「リーチはすればするだけ良い」
麻雀では、リーチをするということは聴牌した(あと1回でアガれる状態になった)ことであり、同時にアガったときの獲得点数も増加します。そのため、リーチをすること自体が得点に直結するかのような言説がしばしばみられます。
しかし、df_gameにおいて、目的関数を得点(point)、所属チーム(team)と選手名(player)を除く他の属性を説明変数とした重回帰分析R1を行ったところ、リーチ数(reach)のp値は高く(約0.380)、有意水準0.1でこの仮説は棄却されました。つまり、リーチをとりあえず数だけ打つこと自体が得点に直結するとはいえないことになります。
言説2:「チームが勝っていれば勝ちやすく、負けていれば負けやすい(流れがある)」
麻雀で代表的なオカルト言説として、「流れ」という概念があります。これは、試合に
「勝ちの流れ」「負けの流れ」があり、この流れに乗ることで、連勝・連敗するという考え方です。この仮説を検証するためには、先ほどの重回帰分析R1において説明変数として前の試合での得点(prev_point)に注目すれば良いでしょう。しかし、R1によれば、prev_point変数のp値も非常に高く(約0.429)、有意水準0.1でこの仮説は棄却されます。つまり、流れがあるとはいえないことになります。
言説3:「順位が低いチームが負けやすく、順位の高いチームは勝ちやすい」
順位が高いチームと順位が低いチームがいるとき、私たちは頻繁に「どうせ順位が高いチームが勝つだろう」と思うことがあります。この思い込みを検定するためには、同じく重回帰分析R1におけるチームの持ち点(team-point)やチーム順位(team-order)のp値を見れば良いでしょう。この値はいずれも0.1より大きく(ともに0.4以上)、この仮説は有意水準0.1で棄却されます。つまり、順位が低いから負ける、順位が高いから勝つと決めつけるのはあまり得策ではないでしょう。
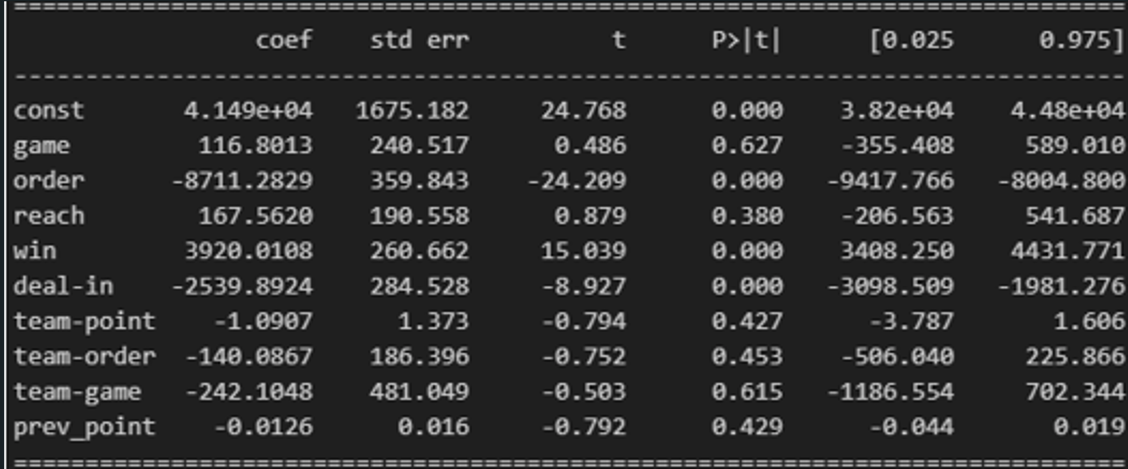 <参考> 重回帰分析R1のサマリー
<参考> 重回帰分析R1のサマリー
以上、この節では麻雀でよく見られる言説に対して統計的な仮説検定を適用して、その真偽を確かめました。ここからわかるように、私たちが日ごろ直感的に信じがちな言説は、必ずしも的を射ているとは言えないと考えられます。戦略的な意思決定を行う際に、統計的な分析を行うことで、こういったオカルト的な穴に陥るリスクを減らすことができることは、十分な意義を持つでしょう。
3. 選手データの主成分分析
次に、選手データdf_playerについて、チーム名と選手名を除いた属性を用いて主成分分析PCA1を実施しました。ここでは、得られた主成分負荷量を分析することで麻雀プレイヤーを分類するうえでの特徴量を発見すること、Mリーグにおけるチーム編成のコンセプトなどを考察することを目的としました。
PCA1によって得られた主成分負荷量は以下のような値になりました。ここではPC1~PC3までで累積寄与率が0.7を超えることから、この3つの主成分の主成分負荷量に注目して解釈することとします。
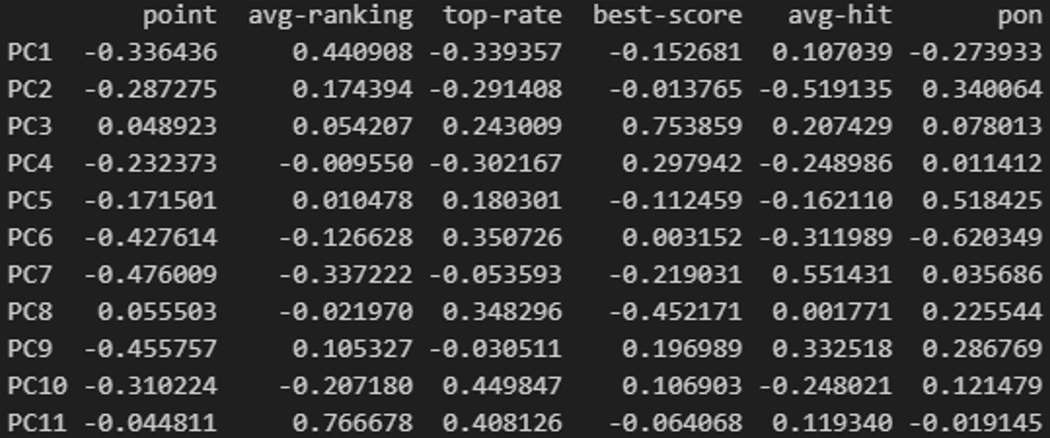 <参考> 主成分分析PCA1の主成分負荷量
<参考> 主成分分析PCA1の主成分負荷量
(ア)PC1の解釈
PC1には、得点・平均順位・トップ率・和了率・放銃率・ラス回避率が主に関係し、平均順位が低いほど、放銃率が高いほど値が大きくなり、得点が高いほど、トップ率が低いほど、和了率が低いほど、ラス回避率が低いほど値が小さくなることが示唆されています。このことから、PC1は順位や点数に関係する主成分であり、「勝ててない度(強さ)」を表していると解釈できます。
(イ)PC2の解釈
PC2には、平均打点・鳴き率・リーチ率・平均放銃点数が主に関係し、鳴き率が高いほど、平均放銃打点が高いほど値が大きくなり、平均打点が高いほど、リーチ率が高いほど値が小さくなっています。このことから、PC2はどれだけ積極的に打つか関係する主成分であり、「積極的度」を表していると解釈できます。
(ウ)PC3の解釈
PC3には、最高得点が強く関係し、トップ率・ラス回避率や放銃率・平均放銃打点が関係しています。そして、最高得点が高いほど、トップ率が高いほど、放銃率・平均放銃打点が高いほど、ラス回避率が低い(ラス率が高い)ほど、値が大きくなっています。このことから、PC3は打ち方の安定性に関係する主成分であり、「不安定度」を表していると解釈できます。
この解釈に基づけば、麻雀プレイヤーの型を特徴づける要素は「強さ」「積極性」「安定性」の3つであり、これは私たちの感覚にも近いのではないでしょうか。
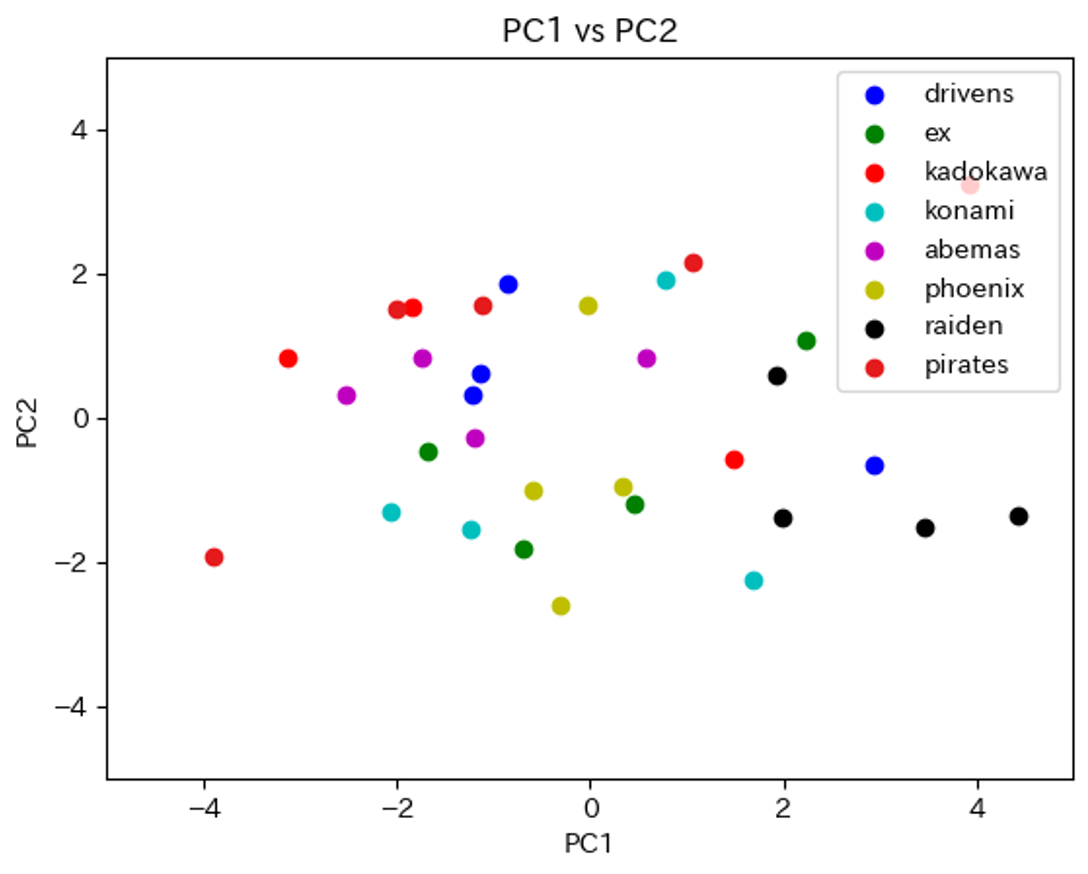
ここで抽出した主成分PC1~PC3を用いて、各選手データを所属チームで色分けした散布図を見てみましょう。


このように選手の特徴を可視化することで、各チームのコンセプトや現状の選手の特徴を直感的に把握することができます。例えば、この主成分分析結果を用いると、raidenとabemasの2チームは比較的似た選手を集めたコンセプトチームであり、piratesやexはバラバラの選手を集めたバランス型チームであることも読み取ることができるでしょう。主成分分析やクラスタリングからも様々な発見があると考えられます。
4. おわりに
この記事では、Mリーグを題材に麻雀のデータを統計的に分析することで、どのような価値が生み出せるか考察してきました。結局のところ、データを用いるのは特定の目的の達成のためであるため、目的を設定すること、その目的に合った手段を選択することが最も重要であるでしょう。一方で、そもそものデータが不足していることで、データを利用しようとしてもできないことがある(現に、今回の分析のために私はMリーグの試合を全試合見返しました)と考えられるため、まずはデータを集積すること、そしてデータを使えばこんなに色んなことの役に立つという認識を広めることが肝心ではないでしょうか。
小宮 雅史 2024年5月9日





